Архив рубрик | ITSec.Ru

10.1. Схема классической электронной подписи

Схемы контроля целостности, рассмотренные в разделе 3.8, могут использоваться только при взаимодействии доверяющих друг другу сторон. Они принципиально не способны обеспечивать улаживание возникающих между ними противоречий и разногласий. Такая возможность появляется только при использовании односторонних функций с секретом для формирования электронной или цифровой подписи.

с помощью электронной подписи получатель документа может доказать, что он принадлежит отправителю, при этом автор подписи не сможет оспорить факт отправки подписанного документа;
электронную подпись невозможно подделать, только абонент, чья подпись стоит на документе, мог подписать данный документ;
электронная подпись является неотъемлемой частью документа, перенести ее на другой документ нельзя;
ни противник, ни получатель не могут изменить документ, оставив данный факт незамеченным;
любой пользователь, имеющий образец подписи, может удостовериться в подлинности документа.

Для повышения надежности схемы электронной подписи, например для противодействия атакам перехвата и повтора сообщений, фальсификации времени отправки сообщений, ее можно сделать зависимой от неповторяющегося блока данных nrb.

Схема электронной подписи включает в себя:

Подпись 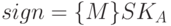$sign = {M}SK_A$

В общем случае неинтерактивный протокол электронной подписи имеет следующий вид.

Схема электронной подписи документа M.

Отправитель А вычисляет
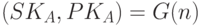
и посылает 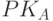получателю В, сохраняя 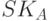в секрете.
Для получения подписи документа M отправитель А вычисляет

и посылает M и sign получателю В.
Получатель В вычисляет
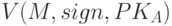
и в зависимости от результата принимает или отвергает подпись sign сообщения M.

В классической схеме электронной подписи, приведенной на
рис.
3.34, предполагается, что подписывающий (абонент А) знает содержание документа M, который он подписывает; проверяющий (абонент В), зная открытый ключ проверки подписи, может проверить правильность подписи в любое время без какого-либо разрешения или участия претендента А.

При создании электронной подписи по классической схеме претендент А выполняет следующую последовательность действий:

применяет к исходному сообщению M хеш-функцию h и формирует хеш-образ сообщения h (M) (при необходимости дополняя входную информационную последовательность до требуемой длины);
при необходимости дополняет хеш-образ до требуемой длины, формируя h* (M) = ext h (M);
вычисляет электронную подпись sign с использованием несимметричного криптоалгоритма D и секретного ключа создания подписи :
$sign = {h* (M)} SK_A$ .

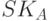Хеш-функция является неотъемлемой частью схем электронной подписи. Применение медленных несимметричных криптоалгоритмов для преобразования всего исходного сообщения M нерационально, поэтому для повышения быстродействия схемы перед процедурой формирования подписи используется функция необратимого сжатия информации.

Последовательность действий абонента В, получившего подписанное сообщение:

верификатор В применяет к тексту полученного сообщения хеш-функцию; дополняет в случае необходимости хеш-образ сообщения до требуемой длины (на
рис.
3.34 рассматривается случай, когда расширение ext h (M) не требуется);
применяет к полученной подписи sign несимметричный криптоалгоритм E с использованием открытого ключа проверки подписи 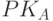и сравнивает полученное значение $PK_A{sign}$ с найденным на предыдущем шаге h* (M), при положительном результате сравнения подпись признается, в противном случае отвергается.

10.3. Secure Hash Algorithm (SHA)

Алгоритм SHA является частью стандарта SHS (Secure Hash Standard), принятого в 1993 г. Национальным институтом стандартов и технологий США (NIST) и Агентством национальной безопасности США. SHA использует принципы, предложенные ранее Р. Ривестом при разработке своих алгоритмов MD4 и MD5.

Рассмотрим версию SHA-1, в которой осуществляется преобразование информационной последовательности произвольной длины в хеш-образ разрядностью 160 бит.

На первом этапе информационная последовательность дополняется до длины, кратной 512 битам. Сначала информационная последовательность дополняется до длины на 64 двоичных разряда меньшей числа, кратного 512: к концу последовательности (сообщения) приписывается 1, а затем необходимое количество нулей. После этого приписывается 64-разрядный код длины сообщения. Если длина исходного сообщения больше 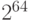$2^{64}$

Пусть после дополнения получена информационная последовательность

На вход i-го основного цикла SHA_i $SHA_{i – 1}$

Перед началом каждого цикла соответствующий блок расширяется до 80 слов по 32 разряда в каждом. Расширение происходит следующим образом. Допустим,

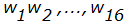
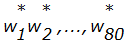
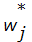
Архив рубрик | ITSec.Ru

Перед началом первого цикла инициализируются пять 32-разрядных переменных

A = 67452301h; B = EFCDAB89h; C = 98BADCFEh;

D = 10325476h; E = C3D2E1F0h,

при этом стартовый вектор хеширования (синхропосылка) есть результат конкатенации этих переменных, т.е.:

Конкатенация новых значений этих переменных, полученных в конце i-го цикла, объявляется результатом работы цикла SHA_i
рис.
3.35.

В начале каждого цикла создаются копии входных переменных:

Затем выполняется 80 шагов алгоритма, на каждом из которых происходит выполнение следующих операций:

В первом раунде (при j = 1, …, 20) используются функция

и константа

во втором раунде (при j = 21, …, 40) используются функция

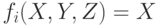
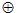
f_i (X, Y, Z) = X Архив рубрик | ITSec.Ru

и константа

в третьем раунде (при j = 41, …, 60) используются функция

и константа

в четвертом раунде (при j = 61, …, 80) используются функция

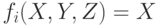
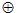
f_i (X, Y, Z) = X Архив рубрик | ITSec.Ru

и константа

Цикл завершается сложением по модулю $2^{32}$

конкатенация полученных значений A, B, C, D и E является результатом работы основного цикла.

В настоящее время существуют версии алгоритма SHA-256, SHA-384, SHA-512.

11.3. Хранение ключей

Секретные ключи не должны храниться в памяти в явном виде, допускающем их считывание. Любая информация об используемых ключах должна храниться в зашифрованном виде, а значит, в защищенной системе должна иметь место иерархия ключей: либо двухуровневая (ключи шифрования ключей – ключи шифрования данных), либо трехуровневая (главный или мастер-ключ – ключи шифрования ключей – ключи шифрования данных).

Учитывая, что такое разделение функций необходимо для обеспечения максимальной безопасности, каждый из указанных типов ключей, различающихся по последствиям компрометации, времени жизни, а иногда и по способам формирования, должен использоваться только по своему прямому назначению.

На самом нижнем уровне иерархии находятся ключи шифрования данных или сеансовые ключи, которые используются для шифрования пересылаемых сообщений или аутентификационной информации. Для защиты сеансовых ключей при их хранении и передаче используются ключи следующего уровня – ключи шифрования ключей.

Учитывая главенствующую роль в иерархии мастер-ключа, используемого в течение длительного времени, его защите уделяется особое внимание:

Один из способов аутентификации мастер-ключа показан на
рис.
3.37.

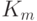
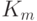
Мастер-ключ – K_m $C = K_m{M}$ K_m $K_m {K_S}$ K_S K_m
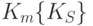
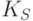
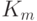
рис.
3.38 приведена схема защиты ключа.Сеансовый ключ – 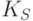K_S $K_m {K_S}$

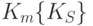
Проще всего хранить ключи криптосистемы с одним пользователем. В распоряжении последнего один из следующих вариантов в порядке возрастания надежности:

Следует помнить, что в первых двух случаях объем ключевого пространства зависит не только от длины пароля или ключевой фразы, но и от ограничения на вид используемых символов. В таблице 3.3 приведено количество возможных ключей при использовании 8-символьной ключевой фразы и время полного перебора при скорости перебора 106 ключей в секунду в зависимости от ограничений на используемые символы.

Также следует помнить о возможности проведения противником так называемой атаки со словарем, включающем в себя наиболее вероятные ключевые слова. Пароли и символьные строки начального заполнения генератора ПСП следует выбирать случайным образом, а не только на основе критерия простоты запоминания.

В последнем случае ни сам ключ, ни исходная информация, необходимая для его получения, пользователю неизвестны, а значит, он не может и скомпрометировать их. Использование ROM-key, имеющего тот же вид, какой имеет привычный ключ от входной двери, позволяет пользователю чисто интуитивно избегать многих ошибок, связанных с хранением криптографических ключей.

14. Причины ненадежности криптосистем

В настоящее время криптографические методы защиты используются в информационных системах любой степени сложности и назначения. Криптографическими методами защищается государственная тайна, обеспечивается законность электронного документооборота, предотвращаются попытки мошенничества в системах электронной торговли.

Современная криптография предоставляет все необходимые алгоритмы, методы и средства, которые позволяют построить систему защиты, затраты на взлом которой таковы, что у противника с ограниченными финансовыми и техническими возможностями для получения интересующей его информации остаются две только две возможности – использование, во-первых, человеческого фактора, а во-вторых, особенностей конкретной реализации криптоалгоритмов и криптопротоколов, которая чаще всего оставляет желать лучшего.

Именно такой вывод можно сделать, анализируя примеры реальных успешных атак на криптосистемы. Известны лишь единичные случаи взлома с использованием исключительно математических методов. В то же время различных примеров взломов реальных систем так много, что их анализом вынуждены заниматься целые компании, наиболее известная из которых Counterpane Systems Б. Шнайера.

Система защиты в целом не может быть надежнее отдельных ее компонентов. Иными словами, для того чтобы преодолеть систему защиты, достаточно взломать или использовать для взлома самый ненадежный из ее компонентов. Чаще всего причинами ненадежности реальных систем криптографической защиты являются:

Самое ненадежное звено системы – человек. Типичные ошибки пользователей, нарушающих безопасность всей системы защиты:

Получают распространение атаки типа отказ в обслуживании (denial of service), провоцирующие пользователя отключать “заедающую” систему защиты при решении неотложных задач.

Можно выделить следующие причины ненадежности криптосистем, связанные с особенностями их реализации:

В некоторых случаях, особенно в системах реального времени, применение стойких алгоритмов принципиально невозможно в силу их низкого быстродействия, и поэтому вынужденно используются менее стойкие, но быстрые криптоалгоритмы.

Многие качественные криптографические средства подпадают под действие экспортных ограничений, искусственно снижающих качество этих средств. Например, в США запрещен экспорт криптоалгоритмов с длиной ключа более 56 бит.

Все программные средства, произведенные в США и легально экспортируемые за рубеж, обеспечивают ослабленную криптографическую защиту. Аналогичная ситуация имеет место и в Европе. Так, например, существуют две версии алгоритма поточного шифрования А5 (стандарт GSM) – надежная А5/1 и существенно менее стойкая А5/2 для поставок в развивающиеся страны.

Многие разработчики ПО включают в свои продукты собственные криптоалгоритмы, самонадеянно считая себя специалистами, забывая, что современная криптография основана на глубоких исследованиях в таких разделах математики, как высшая алгебра, теория чисел, теория информации, теория сложности вычислений и др.

Основные ошибки при применении криптоалгоритмов: недостаточная длина ключа, некачественная процедура управления ключами, некачественный генератор ПСП или неправильная его инициализация; и наконец, использование криптоалгоритмов не по назначению, например хранение паролей в зашифрованном, а не в хешированном виде и использование на практике модели доверительных отношений, отличной от той, в расчете на которую проектировалась система.

Ошибки в реализации криптоалгоритмов. Эта причина ненадежности криптосистем в силу своей нетривиальности и многообразия требует отдельного рассмотрения, поэтому ограничимся лишь кратким перечислением основных проблем, возникающих при реализации криптоалгоритмов.

Надежная система защиты должна уметь оперативно обнаруживать несанкционированные действия для минимизации возможного ущерба. В случае обнаружения повреждений в системе должны включаться эффективные процедуры восстановления разрушенных элементов. Система не должна потерять живучесть даже в случае проведения успешной атаки на нее.

Причины наличия большинства “дыр” (или люков) в ПО, т.е. не описанных в документации возможностей работы с ним, очевидны: забывчивость разработчиков, которые в процессе отладки продукта создают временные механизмы, облегчающие ее проведение, например, за счет прямого доступа к отлаживаемым частям программы. По окончании отладки часть “дыр” убирается, а о части разработчики благополучно забывают либо оставляют их сознательно, особенно в ранних версиях продукта, когда в будущем весьма вероятна его доработка.

“Дыры” могут являться следствием применения технологии разработки программ “сверху вниз”, когда программист сразу приступает к написанию управляющей программы, заменяя предполагаемые в будущем подпрограммы “заглушками”, имитирующими реальные подпрограммы или просто обозначающими место их будущего подсоединения.

Очень часто эти “заглушки” остаются в конечной версии программы. Либо опять же по причине забывчивости, либо в расчете на будущую модификацию продукта, либо, например, если в процессе разработки выясняется, что какая-то подпрограмма не нужна, а удалить заглушку не представляется возможным.

Третий источник “дыр” – неправильная обработка (или ее отсутствие) каких-либо нестандартных ситуаций, которые могут иметь место при работе программы: неопределенный ввод, ошибки пользователей, сбои и т.п. В этом случае противник может искусственно вызвать в системе появление такой нестандартной ситуации, чтобы выполнить нужные ему действия.

Наконец, известны случаи, когда люк в ПО или аппаратуре – первый шаг к атаке системы безопасности. Разработчик умышленно оставляет его в конечном продукте, чтобы в будущем, например, иметь возможность модифицировать информацию незаметно для законного пользователя, расшифровывать ее, не зная ключа, и т.п.

Существуют программы, изначально предназначенные для разрушительных действий: это компьютерные вирусы, компьютерные черви, троянские программы и пр. С полным на то основанием они получили обобщенное название разрушающих программных воздействий (РПВ).

РПВ могут выполнять одно или несколько из перечисленных действий, опасных для системы защиты:

Еще более разнообразны пути внедрения РПВ. Можно выделить следующие средства, предназначенные для борьбы с РПВ, без которых любая программная реализация криптоалгоритма практически беззащитна:

Аппаратуру легче физически защитить от проникновения извне. Криптомодули могут помещаться в особые контейнеры, которые делают невозможным изменение алгоритма функционирования. Интегральные схемы могут покрываться специальным химическим составом, при этом любая попытка преодоления защитного слоя приводит к самоуничтожению их внутренней логической структуры. Тем не менее известны случаи выявления и аппаратных закладок.

Кроме того, возникает проблема защиты от экзотических атак, применимых к реализациям в смарт-картах, – временного анализа и анализа потребляемой мощности. Эти атаки основаны на использовании того факта, что различные операции, выполняемые на микропроцессоре, требует разного времени, а также приводят к разному потреблению мощности.

Приблизительный анализ уязвимости различных операций с точки зрения временных характеристик дает следующие результаты.

Поиск по таблицам – неуязвим для временных атак.
Фиксированные сдвиги – неуязвимы для временных атак.
Булевы операции – неуязвимы для временных атак.
Сложение/вычитание – трудно защитить от временных атак.
Умножение/деление – наиболее уязвимые для временных атак операции.

Стойкость к атакам такого рода, направленным не на криптоалгоритм, а на его реализацию, также надо учитывать. Защищенность по отношению к временному анализу можно повысить путем введения дополнительных задержек. Более сложной является проблема защиты от анализа мощности, но ее можно решить несколькими путями.

С недавних пор получили распространение атаки на аппаратуру криптосистем, основанные на анализе электромагнитного излучения и других побочных источников информации.

Получают распространение по сути “биологические” методы взлома, рассматривающие криптосистемы как сложные объекты, определенным образом реагирующие на внешние раздражители. Атаки подобного рода основаны на анализе поведения системы после случайных или преднамеренных сбоев в работе.

Несмотря на успехи современной криптографии, задача построения надежной системы криптографической защиты комплексная, она значительно сложнее, чем кажется на первый взгляд. Надежная система защиты может быть построена только с учетом всех перечисленных факторов.

К моменту выхода этого курса в большинстве существующих систем обеспечения безопасности произойдет замена криптоалгоритмов с секретным и открытым ключом на лучшие на сегодняшний день – соответственно AES и ECCS, которые были описаны в данной главе.

Поэтому в последующих главах везде, где будет идти речь об алгоритмах блочного шифрования DES, Triple DES (3DES) и других, следует учитывать скорее всего уже свершившийся переход к AES; везде, где речь идет об алгоритме открытого шифрования RSA, следует учитывать скорее всего уже свершившийся переход к ECCS.

4.3. Классификация методов шифрования информации

Основные объекты изучения классической криптографии показаны на
рис.
3.4, где А и В – законные пользователи, W – противник или криптоаналитик. Учитывая что схема на
рис.
3.

Процедуры зашифрования E (encryption) и расшифрования D (decryption) можно представить в следующем виде:

Функции за- и расшифрования взаимно обратные, иначе говоря, для любого текста X справедливо:

На
рис.
3.5 приведена классификация методов шифрования информации. Различают два типа алгоритмов шифрования симметричные (с секретным ключом) и асимметричные (с открытым ключом). В первом случае обычно ключ расшифрования совпадает с ключом зашифрования, т.е.

либо знание ключа зашифрования позволяет легко вычислить ключ расшифрования. В асимметричных алгоритмах такая возможность отсутствует: для зашифрования и расшифрования используются разные ключи, причем знание одного из них не дает практической возможности определить другой. Поэтому, если получатель А информации сохраняет в секрете ключ расшифрования 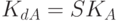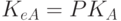$K_{dA} = SK_A$ $K_{eA} = PK_A$ SK – secret key, PK – public key).

В процессе шифрования информация делится на порции величиной от одного до сотен бит. Как правило, поточные шифры оперируют с битами открытого и закрытого текстов, реже – с байтами, а блочные – с блоками фиксированной длины. Главное требование к блочному шифру – высокая криптостойкость.

Блочный криптоалгоритм для своей работы требует наличия полного блока данных, в поточных же криптоалгоритмах стараются обеспечить шифрование в режиме рельного времени или близком к нему (иногда с ущербом для криптостойкости). Но главное различие между этими двумя методами заключается в том, что в блочных шифрах для шифрования всех порций используется один и тот же ключ, а в поточных – для каждой порции используется свой ключ той же размерности.

Иначе говоря, в поточных шифрах имеет место зависимость результата шифрования порции информации от ее позиции в тексте, а в некоторых случаях и от результатов шифрования предыдущих порций текста.
Таким образом, при реализации поточной криптосистемы возникает необходимость в элементах памяти, изменяя состояние которых, можно вырабатывать последовательность (поток) ключевой информации. Блочную же криптосистему можно рассматривать как зависящую от ключа замену на множестве значений блоков открытого текста.

Высокая скорость работы поточных шифров определяет область их использования – закрытие данных, требующих оперативной доставки потребителю, например аудио- и видеоинформации. Учитывая, что при применении классических блочных шифров одинаковым блокам открытого текста соответствуют одинаковые блоки шифротекста, что является серьезным недостатком, на практике получили наибольшее распространение комбинированные методы шифрования (а точнее, поточные режимы использования блочных шифров), использующие сцепление блоков или принцип формирования потока ключей (гаммы шифра) с помощью так называемых генераторов псевдослучайных последовательностей (ПСП), в качестве функции обратной связи которых используется функция зашифрования блочного шифра.

Блочные итерационные шифры. Принцип работы всех современных блочных шифров суть многократное повторение одной и той же раундовой операции. В некоторых случаях раундовые ключи получаются из ключа всей системы с помощью алгоритма выработки раундовых ключей (при этом размер ключа системы существенно меньше суммарного размера всех раундовых ключей).

Идея, лежащая в основе итерационных блочных шифров, состоит в построении криптостойкой системы путем многократного применения относительно простых криптографических преобразований, в качестве которых К. Шеннон предложил использовать преобразования замены (подстановки) (substitution) и перестановки (permutation); схемы, реализующие эти преобразования, называются SP-сетями. Действие таких шифров аналогично “алгоритму”, к которому прибегают, когда месят тесто:

Многократное использование этих преобразований, приведенное на
рис.
3.6, позволяет обеспечить два свойства, которые должны быть присущи стойким шифрам: рассеивание (diffusion) и перемешивание (confusion) информации.

Рассеивание и перемешивание предполагают:

Наличие у шифра этих свойств:

Самые известные блочные шифры – DES (Data Encryption Standard), старый американский стандарт шифрования, созданный в 1974 г., де-факто многолетний неофициальный мировой стандарт шифрования; российский стандарт криптозащиты ГОСТ 28147-89 и новый американский стандарт шифрования AES (Advanced Encryption Standard), принятый в 2001 г. в результате многолетнего открытого международного конкурса.

Структура раундового преобразования DES и ГОСТ носит название петли Фейстеля, схема которой приведена на
рис.
3.7, а структура функций за- и расшифрования – сеть Фейстеля. Структура AES носит название “Квадрат”.

DES работает с блоками данных разрядностью 64 бита с использованием 56-разрядного ключа, из которого по специальному фиксированному алгоритму, использующему перестановки и сдвиги, вырабатываются раундовые ключи. Применяемые преобразования – поразрядное сложение по модулю 2, подстановки и перестановки, число раундов равно 16, перед началом первого раунда выполняется начальная фиксированная перестановка IP, после 16-го раунда выполняется обратная перестановка 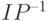$IP^{–1}$

Интересно отметить, что в первоначальной схеме, предложенной IBM, все шестнадцать 48-разрядных раундовых ключей выбирались независимо, т.е. размер ключа был равен 768 битам. Однако по требованию Агентства национальной безопасности США (АНБ), во-первых, размер ключа был уменьшен до 64 бит, из которых только 56 являются секретными, во-вторых, в алгоритме определены перестановки лишь специального вида, не зависящие от ключа, что наводило критиков этого алгоритма на мысль, будто АНБ могла использовать известные ей слабости алгоритма для его взлома.

Существует несколько предложений, направленных на усовершенствование DES. Наиболее известное из них, Triple DES, заключается в трехкратном применении алгоритма.

ГОСТ 28147-89. Ключевая информация ГОСТа представляет собой два массива данных: собственно ключ K и таблицу замен H. Ключ – это массив из восьми 32-разрядных элементов 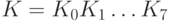K = K_0 K_1 … K_7

В качестве исходных данных раундовая функция шифрования ГОСТа получает 64-разрядный блок данных D = (L, R) и 32-разрядный раундовый ключ, в качестве которого используется один из элементов ключа Кi. В ходе выполнения преобразования левая L и правая R половины блока данных рассматриваются как отдельные 32-разрядные элементы данных, в качестве которых они подвергаются следующим преобразованиям:

сложение по модулю $2^{32}$ полублока R и элементом ключа;
разбиение результата S на восемь четырехбитовых блоков, поблочная замена по таблице замен, формирование из получившихся блоков нового значения S;
циклический сдвиг результата S на 11 разрядов влево;
поразрядное сложение по модулю 2 (XOR) результата S и полублока L;
элемент R становится новым значением элемента L, значение результата предыдущей операции становится новым значением элемента R.

Полученные значения элементов L и R выдаются в качестве результата шага раундового преобразования.

ГОСТ 28147-89 определяет три режима шифрования данных (простая замена, гаммирование и гаммирование с обратной связью) и режим выработки имитоприставки (кода аутентификации сообщений).

4.4. Абсолютно стойкий шифр. Гаммирование

Простейшей и в то же время наиболее надежной из всех схем шифрования является так называемая схема однократного использования, приведенная на
рис.
3.8, изобретение которой чаще всего связывают с именем Г.С. Вернама.

Формируется m-разрядная случайная двоичная последовательность – ключ шифра, известный отправителю и получателю сообщения. Отправитель производит побитовое сложение по модулю 2 ключа и m-разрядной двоичной последовательности, соответствующей пересылаемому сообщению:

Процесс расшифрования сводится к повторной генерации ключевой последовательности и наложения ее на зашифрованные данные. Уравнение расшифрования имеет вид:

К. Шенноном доказано, что, если ключ является фрагментом истинно случайной двоичной последовательностью с равномерным законом распределения, причем его длина равна длине исходного сообщения, и используется этот ключ только один раз, после чего уничтожается, такой шифр является абсолютно стойким, его невозможно раскрыть, даже если криптоаналитик располагает неограниченным запасом времени и неограниченным набором вычислительных ресурсов.

Действительно, противнику известно только зашифрованное сообщение С, при этом все различные ключевые последовательности K возможны и равновероятны, а значит, возможны и любые сообщения M, т.е. криптоалгоритм не дает никакой информации об открытом тексте.

Целью противника может являться раскрытие криптосистемы, нахождение ключа, в крайнем случае, дешифрование какого-либо закрытого сообщения. Однако он может быть удовлетворен, получив даже некоторую вероятностную информацию об исходном тексте сообщения.

Например, известный криптоаналитику факт написания текста некоторого сообщения на английском языке предоставляет ему некоторую априорную информацию об этом сообщении даже до анализа шифровки. В этом случае он заранее знает, что слово “HELLO” является более вероятным началом сообщения, чем набор букв “FGHKM”.

Поэтому одной из целей криптоанализа может являться увеличение информации, относящейся к каждому возможному сообщению таким образом, чтобы правильный текст был более вероятен. Предположим, противник перехватил шифровку “ABCCD” и знает (или предполагает), что использованный шифр – это шифр простой замены.

Анализ шифровки позволяет сделать вывод, что исходное сообщение состоит из пяти букв, причем на третьей и четвертой позициях стоит одна и та же буква, а остальные отличны от нее и различны между собой. Противник не может считать, что это сообщение “HELLO”, потому что имеются и другие возможные сообщения, например “TEDDY”.

Однако апостериорные вероятности таких открытых текстов возрастают относительно их априорных вероятностей. В то же время апостериорная вероятность таких открытых текстов, как “PEACE” или “GATES”, снижается до нуля вне зависимости от их априорной вероятности. По К.

Необходимые и достаточные условия абсолютной стойкости шифра:

Абсолютная стойкость рассмотренной схемы оплачивается слишком большой ценой, она чрезвычайно дорогая и непрактичная. Основной ее недостаток – это равенство объема ключевой информации и суммарного объема передаваемых сообщений. Применение схемы оправдано лишь в не часто используемых каналах связи для шифрования исключительно важных сообщений.

Таким образом, построить эффективный криптоалгоритм можно, лишь отказавшись от абсолютной стойкости. Возникает задача разработки такого теоретически нестойкого шифра, для вскрытия которого противнику потребовалось бы выполнить такое число операций, которое осуществимо на современных и ожидаемых в ближайшей перспективе вычислительных средствах за разумное время.

Данный результат может быть достигнут при использовании гаммирования, схема которого показана на
рис.
3.9.

Гаммированием называют процедуру наложения на входную информационную последовательность гаммы шифра, т.е. последовательности с выходов генератора псевдослучайных последовательностей (ПСП) G. Последовательность называется псевдослучайной, если по своим статистическим свойствам она неотличима от истинно случайной последовательности, но в отличие от последней является детерминированной, т.е. знание алгоритма ее формирования дает возможность ее повторения необходимое число раз.

Если символы входной информационной последовательности и гаммы представлены в двоичном виде, наложение чаще всего реализуется с помощью операции поразрядного сложения по модулю 2. Надежность шифрования методом гаммирования определяется качеством генератора гаммы.

4.5. Генераторы псевдослучайных последовательностей

Качественные ПСП, являясь по своей сути детерминированными, успешно заменяют во многих приложениях (в первую очередь связанных с защитой информации) случайные последовательности, которые чрезвычайно сложно формировать.

Можно выделить следующие задачи, требующие решения при организации защиты информационных систем:

Во всех рассмотренных случаях генераторы ПСП применяются либо непосредственно, либо косвенно, когда на их основе строятся генераторы случайных последовательностей, генераторы контрольных кодов и хеш-генераторы. Во всех случаях требуются последовательности с равномерным законом распределения.

Можно выделить следующие функции генераторов ПСП в системах защиты информации:

Требования к качественному генератору ПСП:

Непредсказуемость. Данное требование означает, что для противника, имеющего возможность анализировать фрагмент ПСП конечной длины, три задачи вычислительно неразрешимы:

В первых двух случаях самая эффективная возможная стратегия – бросание жребия, в третьем – полный перебор по всему ключевому пространству.

Определенные статистические свойства. Это требование означает, что ни один из существующих статистических тестов не в состоянии обнаружить на выходе генератора какие-либо закономерности статистических зависимостей между различными последовательностями, формируемыми при инициализации генератора случайными значениями.

Принципы построения генераторов ПСП. Можно выделить два подхода при использовании в составе генераторов ПСП нелинейных функций: это использование нелинейной функции непосредственно в цепи обратной связи и двухступенчатая схема, в которой задача первой ступени (по сути счетчика) заключается всего лишь в обеспечении максимально большого периода при данном числе N элементов памяти Q. Во втором случае нелинейная функция является функцией выхода $F_{out}$
рис.
3.10 представлены обе вышеназванные схемы.

Вторую схему следует считать более предпочтительной, так как первая имеет следующие недостатки:

преобразование 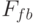$F_{fb}$ является двухпараметрическим, при этом нет никакой гарантии, что при всех значениях секретного параметра K (ключа) формируемая последовательность будет иметь достаточно большой период;
при возникновении ошибки на каком-то шаге выполнения нелинейного преобразования 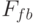$F_{fb}$ искажаются все последующие элементы ПСП.

На
рис.
3.10в показана классификация криптографических генераторов ПСП. Роль нелинейных функций $F_{out}$ $F_{fb}$ $F_{out}$ $F_{fb}$

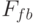
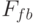
Наиболее обоснованными математически следует признать генераторы с использованием односторонних функций. Непредсказуемость данных генераторов основывается на сложности решения ряда математических задач (например, задачи дискретного логарифмирования или задачи разложения больших чисел на простые множители). Существенным недостатком генераторов этого класса является низкая производительность.

9.4. Схема Kerberos

Решение задачи аутентификации в современных информационных системах, представляющих собой совокупность реализованных на различных аппаратно-программных платформах, территориально разнесенных компонентов, в соответствии с технологией клиент/сервер заключается в использовании специального сервера аутентификации.

В настоящее время на роль фактического стандарта сервера аутентификации претендует Kerberos, продукт разработанный в Массачусетском технологическом институте (MIT) в середине 1980-х гг. и претерпевший с тех пор ряд принципиальных изменений. Широкому распространению Kerberos способствовало то, что его версия, реализованная в MIT, является свободно распространяемым продуктом.

Программные средства, выполняющие аутентификацию по схеме Kerberos, разработаны для всех популярных ОС. Поддержка службы Kerberos предусмотрена в некоторых современных сетевых ОС.
Схема Kerberos является типичным примером реализации симметричных методов аутентификации, она приведена на
рис.
3.33.

Схема предусматривает взаимодействие между тремя программными компонентами – клиентом С, сервером Kerberos и прикладным сервером S. ПО сервера Kerberos разделено по своим функциям на две части: сервер аутентификации AS (Authentication Server) и сервер выдачи разрешений (билетов)

TGS (Ticket Granting Server). Клиент С – это компьютер, на котором установлено клиентское ПО, способное участвовать во взаимодействии по протоколу Kerberos, и зарегистрирован какой-либо пользователь. В некоторых случаях прикладной сервер может являться клиентом некоторого другого сервера, например сервер печати может пользоваться услугами файлового сервера. Сервер S – субъект, предоставляющий ресурсы сетевым клиентам.

Клиент С, который хочет обратиться к прикладному серверу для получения его услуг, должен получить разрешение от AS. Разрешение – это зашифрованная информация, которую клиент передает серверу S или серверу TGS. Разрешение позволяет серверу убедиться в подлинности клиента. Все разрешения, кроме первого, клиент получает от сервера TGS. Первое разрешение, разрешение на доступ к самому TGS, клиент получает от сервера AS. Разрешение – это шифровка, полученная на секретном ключе, известном только серверу S и серверу Kerberos, поэтому первый, получив разрешение, может быть уверен, что оно поступило именно от сервера Kerberos. Разрешения являются многоразовыми, имеющими определенный срок жизни (несколько часов). Когда этот срок истекает, клиент должен вновь пройти процедуру аутентификации. При установлении каждого соединения используется временная метка, поэтому в сети должна действовать служба единого времени.
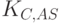
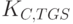
Необходимость в сервере TGS объясняется стремлением сократить число сообщений, зашифрованных с использованием секретного ключа клиента, которому требуются услуги нескольких серверов. Именно поэтому сервер Kerberos “раздваивается” на сервер AS, с которым клиент взаимодействует при помощи секретного ключа $K_{C, AS}$ $K_{C, TGS}$

Процесс аутентификации состоит из пяти (односторонняя аутентификация) или шести (взаимная аутентификация) шагов.

Клиент С посылает серверу аутентификации сообщение, содержащее идентификаторы клиента 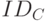и требуемого сервера выдачи разрешений $ID_{TGS}$ , отвечающего за представление соответствующей услуги, а также информацию 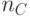, предназначенную для идентификации конкретного запроса: время, свой сетевой адрес и т.п.
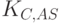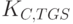Сервер аутентификации осуществляет поиск в базе данных Kerberos по идентификатору клиента и идентификатору услуги, находит соответствующие ключи $K_{C, AS}$ и $K_{AS, TGS}$ , формирует сеансовый ключ $K_{C, TGS}$ для взаимодействия клиента и сервера выдачи разрешений. После этого сервер AS посылает ответ клиенту. Этот ответ содержит две шифровки. 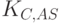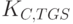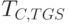Первая, полученная на секретном ключе клиента $K_{C, AS}$ , содержит сеансовый ключ $K_{C, TGS}$ для работы с сервером выдачи разрешений, идентификатор последнего $ID_{TGS}$ и срок жизни $lt_{C, TGS}$ разрешения клиенту на работу с сервером TGS. Вторая шифровка, полученная на ключе $K_{AS, TGS}$ , – это разрешение $T_{C, TGS}$ (ticket-granting ticket) клиенту на взаимодействие с сервером TGS. В состав второй шифровки, которую клиент прочесть не может, так как не знает ключа $K_{AS, TGS}$ ,
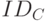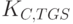входят идентификаторы и $ID_{TGS}$ , сеансовый ключ $K_{C, TGS}$ и срок жизни этого разрешения $lt_{C, TGS}$ .
Получив сообщение, клиент расшифровывает первую его половину на ключе 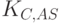$K_{C, AS}$ , проверяет отметку 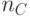, узнает сеансовый ключ 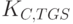$K_{C, TGS}$ и срок жизни разрешения на работу с сервером TGS. Таким образом, в результате обмена сообщениями с сервером AS клиент получает разрешение на работу с сервером TGS. Затем клиент посылает запрос серверу выдачи разрешений. Сообщение для сервера TGS включает в себя две шифровки. Первая, полученная на сеансовом ключе 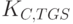$K_{C, TGS}$ , включает в себя идентификаторы 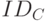и 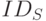, идентификатор запроса 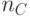и временную метку 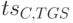$ts_{C, TGS}$ . 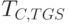Вторая – это “запечатанное” ключом $K_{AS, TGS}$ разрешение $T_{C, TGS}$ .
Сервер выдачи разрешений расшифровывает разрешение 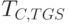$T_{C, TGS}$ , узнает сеансовый ключ 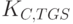$K_{C, TGS}$ , с помощью которого читает первую часть пришедшего сообщения и проверяет идентификатор 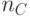и временную метку 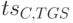$ts_{C, TGS}$ . Удостоверившись в подлинности клиента, сервер TGS вырабатывает сеансовый ключ 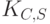$K_{C, S}$ для взаимодействия клиента С и сервера S. На знании этого ключа и будет основываться в будущем взаимная аутентификация C и S. После этого сервер отправляет сообщение клиенту, содержащее зашифрованные на ключе 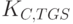$K_{C, TGS}$ сеансовый ключ и срок жизни разрешения клиенту на работу с сервером, а также само это разрешение 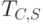$T_{C, S}$ , зашифрованное на секретном ключе $K_{S, TGS}$ .
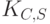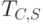Клиент, получив сообщение, расшифровывает первую его часть, из которой извлекает сеансовый ключ $K_{C, S}$ для работы с сервером S и срок жизни разрешения на взаимодействие с сервером S. Само “запечатанное” ключом $K_{S, TGS}$ разрешение $T_{C, S}$ клиент прочесть не может. Таким образом, в результате обмена с сервером выдачи разрешений клиент получает разрешение на дальнейшее взаимодействие уже с прикладным сервером. Наконец, клиент посылает серверу S сообщение, содержащее зашифрованные на сеансовом ключе 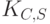$K_{C, S}$ свой идентификатор 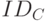, идентификатор 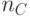и временную метку 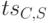$ts_{C, S}$ , а также разрешение 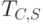$T_{C, S}$ , полученное от сервера TGS.
Приняв сообщение от клиента и “распечатав” разрешение 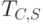$T_{C, S}$ , целевой сервер узнает сеансовый ключ 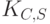$K_{C, S}$ и с его помощью проводит аутентификацию клиента, проверяя идентификатор 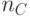и временную метку 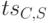$ts_{C, S}$ . Ответ сервера клиенту посылается в том случае, когда требуется взаимная аутентификация. Ответ прикладного сервера в этом случае содержит зашифрованный на ключе 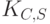$K_{C, S}$ результат преобразования 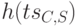$h (ts_{C, S})$ метки $ts_{C, S}$ .

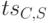Сервер Kerberos имеет доступ к базе данных, содержащей идентификаторы и секретные ключи субъектов. Запись каждого пользователя и каждого прикладного сервера в базе данных Kerberos содержит следующие компоненты:

Секретные ключи субъектов шифруются мастер-ключом Kerberos. Когда секретный ключ изменяется нормальным образом, т.е. не в результате компрометации, то старый ключ следует сохранять до тех пор, пока остаются годными билеты, выданные с его помощью, так как возможна ситуация, когда один субъект имеет несколько активных ключей.

Помимо серверов AS и TGS в системе имеется объект, отвечающий за управление базой данных, называемый диспетчером базы данных Kerberos DBM (Database Manager), а также сервер распространения ключей Kerberos KDS (Key Distribution Server).

9.5. Несимметричные методы аутентификации субъекта

Использование криптосистем с открытым ключом позволяет отказаться от серверов аутентификации, однако в системе должен существовать сервер, выдающий сертификаты на используемые субъектами взаимодействия открытые ключи. Сертификатом принято называть электронный документ, удостоверяющий принадлежность данного открытого ключа данному субъекту, иначе говоря, аутентичность ключа.

Протокол Диффи—Хеллмана. Несимметричные методы аутентификации могут быть основаны на использовании механизма электронной подписи. Классическим примером несимметричной аутентификации может служить схема Диффи-Хэллмана, представляющая собой совокупность процедуры выработки общего секретного ключа и взаимной аутентификации субъектов взаимодействия. Допустим, w – примитивный элемент поля Галуа GF (p), где p – простое число. Абонент А владеет парой ключей: 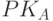PK_A SK_A PK_B SK_B

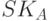
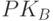
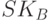
Схема аутентификации Диффи—Хеллмана.

Абонент А вырабатывает случайное число 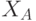и отправляет абоненту В сообщение
(здесь и далее предполагается, что все операции выполняются по модулю p).
Абонент В вырабатывает случайное число 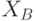, вычисляет 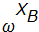, на своем секретном ключе создает подпись
сообщения
Затем В вычисляет сеансовый ключ
зашифровывает подпись на этом ключе и отправляет А сообщение
, ,
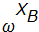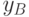где
Абонент А вычисляет сеансовый ключ
с помощью своего секретного ключа создает подпись
сообщения
зашифровывает ее на ключе 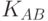$K_{AB}$ и отправляет В сообщение
Если проверка подписи В абонентом А завершилась успешно, т.е. А убедился в справедливости равенства
он может быть уверен в подлинности абонента В.
Если проверка подписи А абонентом В завершилась успешно, т.е. В убедился в справедливости равенства
он в свою очередь может быть уверен в подлинности абонента А.

Протокол Фиата—Шамира. Рассмотрим простейшую схему аутентификации с нулевым разглашением знаний. Подобные протоколы используются интеллектуальными картами. Личность владельца карты признается подлинной, если претендент доказывает свое знание секретного ключа.

Для реализации схемы необходим центр доверия, который выбирает и публикует целое число вида N = pq, где p и q – простые числа, которые держатся в секрете. Предположим, абонент А является доказывающим, абонент В – проверяющим. Абонент А (или центр доверия) формирует открытый и секретный ключи:

и объявляет их открытым ключом 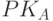PK_A

Протокол аутентификации Э. Фиата и А. Шамира состоит в t-кратном повторении следующих шагов.

Схема Фиата—Шамира.

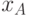
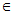
Абонент А выбирает случайное число 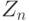, вычисляет
и посылает его В.
Абонент В выбирает случайную двоичную последовательность
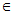{0, 1}, j = 1, …, m
и посылает ее А.
Абонент А вычисляет
и посылает его В.
Абонент В проверяет равенство